
MAT 是什么?
MAT 全称 Mathematics Admission Test,是牛津大学数学和计算机相关专业的必须的入学资格专项考试,具体有:
- 数学
- 数学与统计
- 数学与计算机
- 数学与哲学
- 计算机科学
- 计算机科学与哲学

另外,申请帝国理工和华威大学的数学专业也建议参加 MAT 考试。其中,帝国理工凡是名字里数学开头的专业,都要求在10月15日前递交 UCAS 的申请者必须参加 MAT 考试,在10月15日之后递交的申请者则需要在难度丝毫不亚于 MAT 的 STEP 的考试中获得一等或以上的成绩。
华威大学只是纯数学专业的录取标准中会涉及到 MAT 考试,但并不是必须项。A-Level 考生如果可以考到 A*A*A* 或 A*A*AA 或 A*A*A + STEP 这种硬核成绩,没有 MAT 华威也是会照样录取的。但是优秀的 MAT 考分可以降低录取标准。
MAT 考试时长2.5小时,满分100分。 在规定的时间内,所有参加 MAT 考试的学生都必须完成第1大题的十道选择题(每题4分,小计40分)。后面的6个简答题根据不同的申请专业方向完成4题(每题15分,小计60分)。
- 申请牛津数学、数学与统计、数学与哲学专业的考生,完成 2,3,4,5
- 申请牛津数学与计算机专业的考生,完成 2,3,5,6
- 申请牛津计算机科学、计算机与哲学专业的考生,完成 2,5,6,7
- 不申请任何牛津专业,只申请帝国理工和华威的考生,完成 2,3,4,5
这6个大题没有一成不变的套路。大体的说,第2大题通常是一个代数题;第3题是函数题,经常会结合函数图像和微积分来考学生;第4题是一个几何题;第5题根本无法事先预测,完全不按常理出牌,一般考察逻辑思维;第6题会是跟逻辑推断或是数论相关;而最后的第7题近年来的趋势总是跟算法相关的问题。
下图是一个 MAT 历年考题所涉及知识点的归类,由于很多问题其实涉及多个数学分支领域,所以这个分类非常粗略,仅供参考。
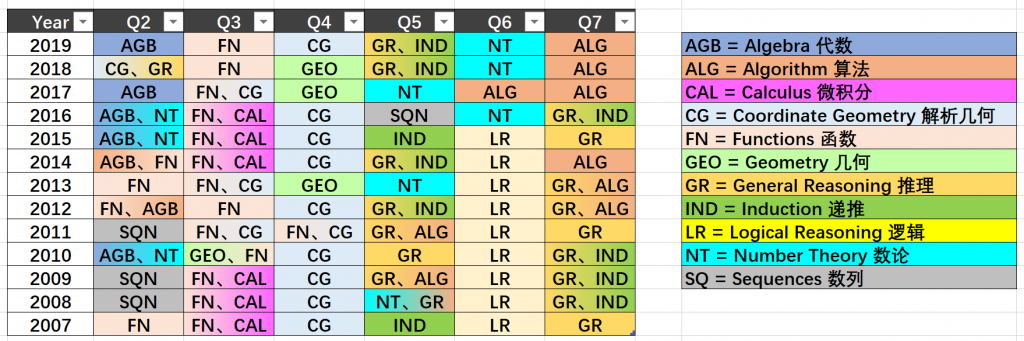
MAT 考什么?
牛津大学给出了 MAT 考试的完整大纲,准备备考的同学们可以打开下面的链接查看。
https://www.maths.ox.ac.uk/system/files/attachments/syllabus_1.pdf
这份大纲文件只有不到一页的篇幅,写的非常简略,我们甚至可以直接在这里贴出来。

总体而言,MAT 数学部分考察的知识点甚至不及 A-Level 普通数学。但是大纲简单并不意味着 MAT 考试就会简单。这主要是出于公平的角度考虑,因为世界上仍有教育欠发达地区没有足够的师资,牛津大学确保潜力苗子不会因为有的东西没机会学而处于劣势。
从某种角度来讲,MAT 考察的并不是学生知道多少高阶的数学知识,更多是考察学生利用现有知识解决难题的能力(problem-solving skills)。 MAT 的问题的解答肯定是比较复杂的,考生要能 get 到题干给出的隐晦的提示,需要一点点来自于自己的灵感,并在此基础上用严谨的逻辑推理,一步一步引到最后的结果。
例如 MAT 很喜欢考函数图像的问题。拿到看起来丧心病狂的复合函数,要构建出它的大致图像其实需要做很多小的分析:
- 在 时的极限行为?
- 在 及其他特殊点的取值?
- 是否存在零点?
- 是否存在渐近线(asymptote)?
- 是否存在极大值、极小值?
- 在不同区间上的单调性?
- 是否存在对称性?周期性?
- 是否可以想象成从熟悉的函数形式得来的某种变换?
胃口较好的读者不妨尝试一下以下的函数图像(均来自 MAT 真题):
- (2011)
- (2012)
- (2009)
- (2008)
- (2014)
- (2010)
- (2007)
- (2016)
- (2015)
- (2019)
- (2013)
- (2018)
- (2009 Specimen)
- (2019)
MAT 历年考题里,也很喜欢让考生来分析一些奇奇怪怪的方程 会有多少根的问题。类似的问题还经常会告诉你某个带参数 的方程的解的个数,让你反推 可能的取值范围;或者给出两条函数曲线,让你找交点的个数。分析这些问题时,可能需要拿出毕生所学的十八般武艺,也许可以很快乐地化成一个二次方程用判别式搞定,也许需要用到换元法来化简方程,也许需要借助函数图像来帮忙,也许需要考虑一下 的极值作为突破口,也许可以通过放缩法处理后发现方程压根没有根。
有胃口的同学可以试着寻思下以下的方程会有多少个根(同样都来自于 MAT 真题):
- (2019)
- (2007)
- (2015)
- (2019)
- (2010)
- (2007)
- (2019)
- (2011)
- (2016)
- (2010)
- (2009)
- (2012)
其他 MAT 中涉及到的技巧性比较强的操作,包括但不限于对称性的应用,利用几何方法来解决代数问题,针对奇偶性的分类讨论,通过递推关系从简单的情形推理到复杂的情形,等等。
MAT 备考建议
很难定义说 MAT 究竟考察申请者哪方面的能力。在这里我只能说是给备考 MAT 的同学一些建议。
MAT 考试没有公示表,所以常用的基本公式务必牢记于胸。 比如
- 等比数列前
- 二项式展开系数:
- 三角函数里的基本恒等式:
- 近似计算定积分的梯形法则公式:
这些在 MAT 考题中要用到时应该能张手就来。
MAT 考试也不允许使用计算器,所以平时练习时也多锻炼一下自己的计算能力,培养对数字的敏感性。 在这里也不妨来小小考一考读者:
- 是多少?
- ,, 都是多少?
- 化简
- 给出 ,, 的近似值
MAT 的选择题只要选出正确选项就能拿分,但是在简答题里,评分中挺大的比重是看论证过程交代的是否清楚。大题中常常会要求考生针对一个小问题做出猜想并给出证明,考生们应当尝试用逻辑清晰的语言给出解释,练习时建议多多操练证明的书写过程。
在一些巧妙设计的问题里,出题人经常会带有引导性地先让考生证明几个小结论,这些其实都是出题人给你送出的隐形助攻。 按上海话讲,考生要能“接领子”:做到后面的小问没有思路时,也要多思考可以如何跟前面得出的小结论建立起联系,常常这就是那个难题的突破口。
常见问题解答
备考 MAT 有什么推荐的刷题资源?
最香的当然是 MAT 真题。 在牛津大学数学系的网站上不仅可以下载到最近十余年的真题,还有官方的标准答案。
https://www.ox.ac.uk/admissions/undergraduate/applying-to-oxford/tests/mat
易天教育辅导 MAT 多年的烤羚羊老师编写有几大专题的授课讲义,还有最近几年的真题的全套手写解答,有兴趣的 MAT 党们欢迎前来咨询。


其次 TUMA 和 STEP 数学考试的真题也是很值得看一看。 这两者也是不少大学数学相关专业接受的专项测试,前者全是选择题的题型,后者全是解答题。从难度上来,大致可以列为:STEP > MAT > TUMA,其中 STEP 还分为 I、II、III 三个难度等级。刷 MAT 尚绝吃力的同学可以尝试从 TUMA 开始打怪升级,MAT 刷完还不过瘾的可以找 STEP 继续修炼。下载传送门如下:
https://www.admissionstesting.org/for-test-takers/step/preparing-for-step/
剑桥大学 Jesus College 的数学讲师 Stephen Siklos 为备考 STEP 的考生写过一本非常详尽的教材,精选了75个问题作了详细的解答,每个题后有很有洞见的点评。这本书的电子版在下面的网址可以免费下载。
https://www.openbookpublishers.com/product/1050

这里再推荐给大家两个业界良心网站。一个叫做 Underground Mathematics ,做了非常细致的分类题库。 打开下面的链接,点击右上角导航栏的 Browse,在 Review Questions 的下拉列表里可以找到 Oxford MAT 的分类题库。
https://undergroundmathematics.org/
还有一个叫做 Maths Helper,网站有一个 Oxbridge Page 的专门页面,一站式到位地整合了 MAT、TUMA、STEP 还有其他有用的真题试卷,但只有2016年以前的资源。
http://www.mathshelper.co.uk/oxb.htm
MAT 需要考多少分?
我们拿数据说话。每年牛津大学会给出 MAT 成绩统计,历年的报告可以在以下网址找到。
https://www.ox.ac.uk/admissions/undergraduate/applying-to-oxford/tests/mat
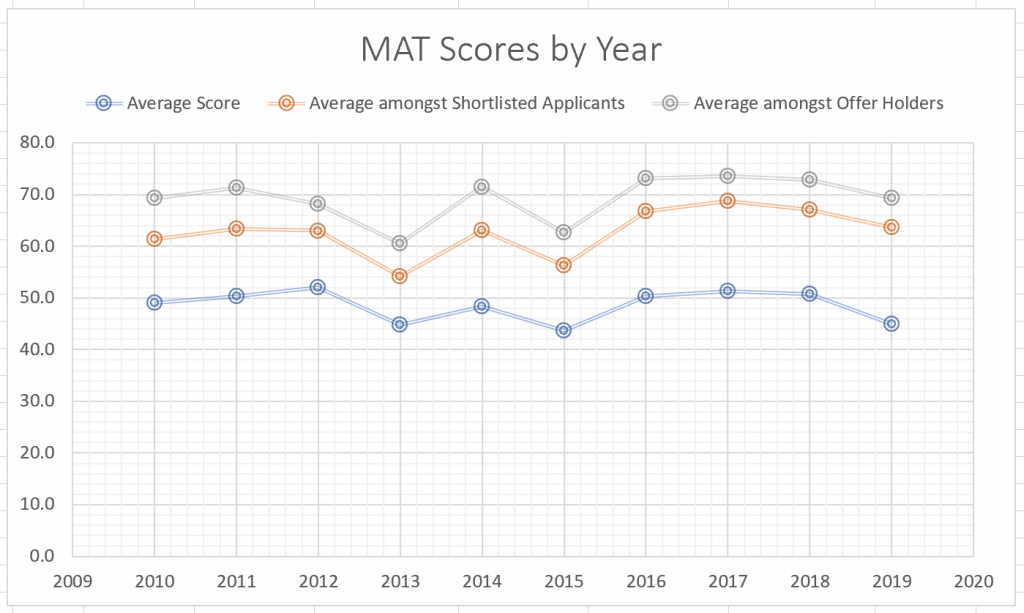
从历年规律来看,MAT 的平均分在50分左右,拿到65分可以大致确保获得面试资格(Short-listing),而最终获得录取的申请者的均分则普遍在70以上。 要从众多申请者中脱颖而出,考分显然是越高越好,因为虽然后续会有一轮重要的面试环节,但决定最终录取与否的是 MAT 笔试和面试的综合表现。这里给出的建议是,有志于牛津数学和计算机的同学,在备考 MAT 时目标应该定在80+。
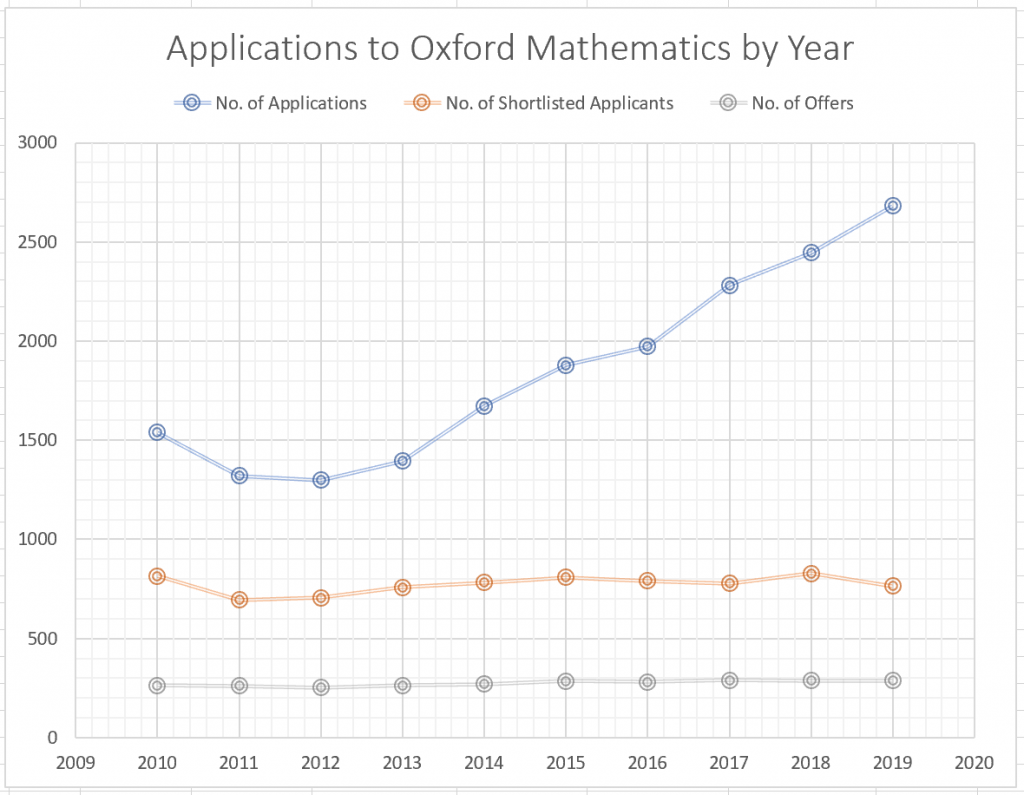
在报告的数据中,我们也可以挖掘出历年申请牛津数学专业的人数和最终录取数。很容易看到,申请者的数量年年走高,2019年的申请总人数比起2011年已经翻了一番,但是最终录取数多年来没有明显变化,可见竞争愈发激烈。这里也祝有志攀登牛津殿堂的勇者们好运!
